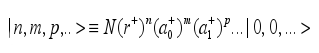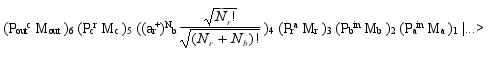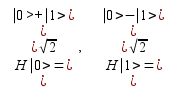Abstract
The field of quantum programming languages is developing rapidly. Research includes the design of programming languages for quantum computing, design of compilers, etc. In this paper our attention is focused on the quantum assembly languages based on the algebraic representation of languages.
1 Introduction
A natural question that arises when one considers quantum computers is whether a quantum machine language exists and what its nature might be. The question about of higher level languages is also relevant. Can we develop a quantum assembly language and exist there equivalents to the languages as C, C++, Java, or C#?
The classical (non – quantum) computer can be viewed in a simplified model as a system having a main memory, register and a central processing unit (CPU) that executes program instructions step by step. A set of data and program (set of instructions) is stored in memory. The CPU executes the program step by step using the data to produce an output set of data. The basic instructions of assembly language moves data values between memory and the registers and provides basic arithmetic and logical operations. A computer has another register called the program counter. The value in the program counter is the memory location of the next instruction to execute. In this article we discuss some aspects of quantum assembly languages with position their algebraic representation.
2 Algebraic Representation of Assembly Language
The view of assembly language is that it has a word consisting number of bits (64-bit computer). Some assembly language programmers would even say that assembly language is english-like oriented to make them easier for programmers.
In this section we follow the opposite course and show that the computer language can be reduced to an algebraic representation. It means that computer language can be represented with creation and annihilation operators [1]. We can develop the algebraic representation for the case of the simple assembly language [2]. It provides better understanding of computer language and quantum computers.
The algebraic representation can be used develop a representation for words consisting of some number of bits using commuting harmonic oscillator-like raising and lowering operators. To establish the algebraic representation we associate a creation operator a+i and annihilation operator ai with each memory location. These operators satisfy the commutation relations
where δij is 1 if i = j and zero otherwise. We also define a pair of creation and annihilation operators for the register r and r+, respectively. To develop a simple algebraic representation of assembly language we will assume the size of a word is so large that it can be viewed as infinitive.
The ground state of the computer is the state with the values at all memory locations set to zero. It is represented by the state vector. A state of the computer will be represented by a vector of the form
where N is a normalization constant and with the first number being the value in the register, the second number the value at memory location 1, and so on. We can set a computer state to have certain initial values in memory a then it evolve by execution a program to a final computer state with a different set of computer values in memory. The program is mapping of the instructions of a assembly language program to algebraic expression by the creation and annihilation operators.
We can define M and P operators to express the algebraic equivalent of assembly language instructions. For example, if we want load the value at memory location m into register, then operators have expression Prm Mr . Store the value in the register at memory location m will be Pmr Mm . Assembly language instructions could be combined to form an assembly language program. It means, that the following an assembly language program
1 INPUT a
2 INPUT b
3 LOAD c
4 ADD b
5 STORE c
6 OUTPUT c
7 HALT
can be translated to the algebraic equivalent [2]
(3)
If we will not to consider superposition of computer states we get classical computer and in the opposite regime we have quantum computer – it depends on a hardware realization.
To create a quantum computer we need have a material which approximates a lattice with spins at each lattice site that we can oriented electromagnetically at the beginnig of a program. The electromagnetic fields implement a set of interaction between spins that simulate the calculation to be performed. The interaction are specified with some Hamiltonian.
However, from a practical point of view may be difficult to create such hardware that would serve to implement the quantum version of the assembly language. We can use a simplified version of the quantum computer, when we have only two parts, the first part is called register, where are located qubits and the second part is counter instructions –program counter. The every instruction could be represented by a system of laser pulses that act defined way on the system ions located in the linear ion trap [3].
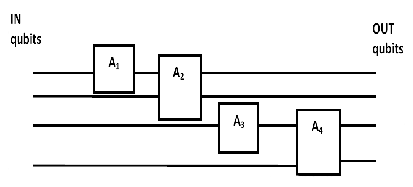
Let G be some sort of operation for example on three ions a, b, and c, which converts the original state |a, b, c> into a next state |a‘, b‘, c‘>. We are not trying to move data from one position to another – we are going to change it. It means
G is an operator or a matrix.
Fig. 1: Application of operators to input qubits can be expressed as a sequence of primitive 1- and 2-qubit operators
The operator G can be expressed in the form of the product of one- and two-qubit operators as it is shown in Figure 1
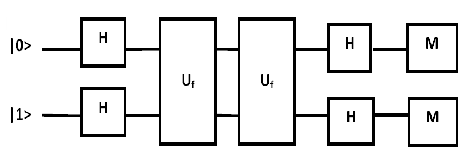
Let take to consider as an example a quantum circuit shown in Figure 2
Fig. 2: The quantum circuit as a sequence of the primitives.
In view of the above proposal can be expressed in the form of the final state
where H is the Hadamard operator
The operator Uf is defined as follows
The operátor is tensor product and the operator corresponds to the XOR operations. If the function f has properties: f(0) = f(1) = 0 we get the following result |F> = |0>|1>. This means that the final state is such that the first qubit with probability p = 1 can be found in the state | 0>.
A quantum computer can be built using single qubit operation and two-qubit CNOT gates because any computation can be decomposed into a sequence of these basic gate operations [4, 5]. It is possible to create primitive gates so that their combined give effect to quantum calculations. In this sense quantum computer is made up of primitive gates which sequentially acts on the qubits in the register.
3 Results and discussion
We could develop the quantum assembly language and to make a basis for high level quantum programming language if we use the algebraic representation of the language. These languages will be quantum analogous to high level computer language such as C language. If we decide to define a high level quantum computer language then it would be natural to define it analogously in terms of a quantum assembly language. A statement in high level quantum computer language would map to a set of quantum assembly language instruction. We have showed that we can develop a simpler representation of quantum computing, in which qubits will not move from one memory to another, they only change their states through the gate operations.
Quantum computation is a new computational model based on the principles of quantum mechanics. Its goal is to solve problems that cannot be solved classicaly efficiently. Quantum computers are the next generation computers. They can perform complex engineering, mathematical and other computations in much less time. Due to certain disadvantages and high price, quantum computers may not currently replace the traditional computers. We believe that after the ongoing researches and developments in the field, we may soon get handy quantum computers.
References
[1] Sudbery A., Quantum Mechanics and the particles of nature: an outline for
mathematicians, Cambridge University Press, 1986.
[2] Blaha, Stephen (2002), Quantum Computers and Quantum Computer
Languages: Quantum Assembly Language and Quantum C.
http://archives.cs.iastate.edu/documents/disk0/00/00/02/66/
[3] Gulde et al., Implementation of the Deutsch-Jozsa algorithm on an ion-trap
quantum computer, Nature 42 (2003) 48-50.
[4] Sleator T., Weinfurter H., Realizable universal quntum logic gates, Phys. Rev. Lett.
74 (1995) 4087-4090.
[5] DiVincenzo D. P., Two-bit gates are univesal for quantum computation, Phys. Rev.
A 51 (1995) 1015-1022.
Autor:
RNDr. Viliam Malcher, CSc.
Pracovisko:
Department of Information Systems
Faculty of Management
Comenius University in Bratislava
Odbojárov 10,
820 05 Bratislava 25,
Slovakia
Recenzenti:
Ing. Jaroslav Vojtechovský, PhD.
Pracovisko: Fakulta managementu UK, Odbojárov 10, Bratislava
prof. RNDr. Michal Greguš, PhD.
Pracovisko: Fakulta managementu UK, Odbojárov 10, Bratislava
Vydanie:
Digital Science Magazine, Číslo 1, Ročník III.